Część i całość. W stronę topoontologii

Przenieśmy się do krainy płaszczaków, czyli krainy stworzonej przez Edwina Abbotta, brytyjskiego pisarza, autora Flatlandii. Wyobraźmy sobie świat złożony z dużej kartki papieru. Jego mieszkańcy, odcinki, trójkąty, kwadraty, pięciokąty i inne figury mogą się swobodnie poruszać po tej kartce, ale nie mogą wyjść ani pod nią, ani ponad nią. Jak płaszczaki widzą siebie nawzajem?

Okrągła moneta na kartce widziana z góry wygląda jak koło, ale im bliżej jesteśmy kartki, im bardziej jesteśmy płaszczakami, tym bardziej figury wyglądają jak odcinki. Z krawędzi stołu każda figura wygląda jak odcinek. Kiedy płaszczak się zbliża do danej figury, to odcinek ten się po prostu wydłuża, kiedy płaszczak się oddala, to odcinek ten robi się krótszy. Dlatego płaszczaki się nie odróżniają, widzą tylko odcinki i nic więcej. Domy płaszczaków powinny zawierać co najmniej 5 boków, ponieważ domy kwadratowe, a tym bardziej trójkątne, posiadają zbyt ostre kąty, co mogłoby doprowadzić roztargnionego przechodnia do poważnego wypadku. W domach nie ma okien, światło oświetla zarówno wnętrza, jak i zewnętrza domów tak samo i bez względu na porę. Źródło światła pochodzi z przestrzeni, ale mieszkańcy Flatlandii nie znają przestrzeni. Uczeni z krainy płaszczaków, którzy próbowali wyjaśnić pochodzenie światła ze świata przestrzeni, trafili do domu dla obłąkanych.

Pewnego razu sfera wyławia kwadrat i zabiera go do przestrzeni. Sfera przechodząca przez Flatlandię widoczna jest początkowo jako punkt, następnie jako odcinek o coraz większych, a następnie coraz mniejszych rozmiarach, aż do zmniejszenia się znów do postaci punktu. Tylko tak sferę mogą widzieć mieszkańcy krainy płaszczaków. Kwadrat, który zobaczył trochę przestrzeni, zdając sobie sprawę z wcześniejszej bardzo ograniczonej, bo całkowicie płaskiej perspektywy, popada w zachwyt nad przestrzenią. Próbuje więc wyjaśnić płaszczakom, czym owa przestrzeń jest. Oczywiście zostaje okrzyknięty heretykiem, bo perspektywa przestrzenna istotnie wychodzi poza ramy perspektywy płaskiej. W świecie jednego wymiaru nikt nie chce słyszeć o świecie o dwóch wymiarach, w świecie dwóch wymiarów nikt nie chce słyszeć o świecie trzech wymiarów, i tak dalej. Niemniej z każdym wymiarem bogactwo możliwych sposobów bycia w przestrzeni wzrasta niepomiernie: w świecie jednowymiarowym mieszkańcy widzą tylko punkty, w świecie dwuwymiarowym widzą już odcinki, a w świecie trójwymiarowym figury posiadające — oprócz długości i szerokości — głębokość.

Doświadczenie niezrozumienia wyższego wymiaru, na przykład powszechne trudności w wyobrażeniu sobie czwartego wymiaru, potwierdzają intuicję Abbotta o wadze wymiaru danej przestrzeni. Wymiar przestrzeni jest własnością topologiczną, co oznacza, mówiąc jeszcze nieściśle, że nie zmienia się po odpowiednio zdefiniowanym przekształceniu danej przestrzeni. Przez to wymiar odróżnia przestrzenie od siebie, na przykład odróżnia prostą od powierzchni, a powierzchnię od przestrzeni trójwymiarowej. Wymiar stanowi różnicę. Jest istotną własnością struktury. Przez strukturę w tej książce rozumiem strukturę topologiczną. Innymi słowy zakładam, że struktura to w istocie topologia, przestrzeń to przestrzeń topologiczna, a immanentne i istotne charakterystyki przestrzeni to niezmienniki przekształceń topologicznych, o których więcej powiem za chwilę.

Książka ta jest przeglądem zagadnień, które z jednej strony dotyczą części i całości, a z drugiej dotykają strukturalnych charakterystyk, czyli własności topologicznych. Ontologia, w której decydujące są własności topologiczne, staje się ontologią topologiczną, w skrócie topoontologią. Filozofię, w której wykorzystuje się przestrzenno-topologiczne własności, nazywam topologiczną filozofią, w skrócie topofilozofią.

*****

Ta przeglądowa monografia jest książką trudną, nawet bardzo trudną. Niemniej jest ona istotnym wkładem w nowopowstającą dziedzinę filozofii, tj. topoontologię. Niewątpliwie wyzwaniem jest zmierzenie się z zaawansowanymi konstrukcjami, które przywołuje Bartłomiej Skowron. Nie waha się on balansować na granicy poznawalności. Kto jednak podejmie trud analizy owych problemów wraz z autorem, z pewnością dostrzeże, że zarówno koncepcje Skowrona, jak i dociekania omawianych przez niego krytycznie filozofów, rzucają nowe światło na wiele tradycyjnych problemów filozoficznych. Cierpliwość i wysiłek Czytelnika zaowocuje. Jestem tego pewien.

dr hab. Janusz Kaczmarek, prof. UŁ

• Autor: Bartłomiej Skowron
• Wydawca: Oficyna Wydawnicza Politechniki Warszawskiej
• Rok wydania 2022
• Liczba stron 370
• Wydawca Oficyna Wydawnicza Politechniki Warszawskiej
• ISBN-13 978-83-8156-279-9

 

[tabs]
[tab title=”Spis treści”]

Spis treści

Wprowadzenie ix

• 0.1 Pierwsze intuicje ix
• 0.2 Metoda: filozofia topologiczna, w skrócie topofilozofia xii
• 0.3 Przegląd treści rozdziałów xvii
• 0.4 Potencjalny odbiorca książki xxiv
• 0.5 Topoontologia w Polsce w XXI wieku xxv
• 0.6 Podziękowania xxvii
• 0.7 Nota redakcyjna xxviii

1. Mereologia 1

• 1.1 Klasyczna mereologia 1
  • 1.1.1 Definicje pomocnicze 2
  • 1.1.2 Suma mereologiczna 3
  • 1.1.3 Twierdzenia klasycznej mereologii 6
  • 1.1.4 Twierdzenie o reprezentacji 8
• 1.2 Mereologia z sąsiedztwem 11
  • 1.2.1 Podstawowe definicje 13
  • 1.2.2 Regiony izolowane i zintegrowane Roepera 15
  • 1.2.3 Metoda rozciągłej abstrakcji Whiteheada 16
  • 1.2.4 Punkty w strukturze MC 18
• 1.3 Inne rachunki 19
• 1.4 Kategoryjna aktualizacja mereologii Thomasa Mormanna 19
  • 1.4.1 Strukturalna mereologia 20
  • 1.4.2 Strukturalna mereologia grup 21
  • 1.4.3 Kategoryjne ujęcie mereologii 28

2. Topologia 33

• 2.1 Wprowadzenie 33
• 2.2 Przestrzeń topologiczna 35
• 2.3 Przestrzenie metryczne 36
  • 2.3.1 Przykłady przestrzeni metrycznych 36
  • 2.4 Wnętrze i domknięcie, zbiór gęsty i brzegowy 38
  • 2.5 Aksjomaty oddzielania 42
• 2.6 Przekształcenia 45
  • 2.6.1 Przekształcenia ciągłe 45
  • 2.6.2 Homeomorfizmy 45
  • 2.6.3 Własności topologiczne 46
• 2.7 Spójność i jej odmiany 48
• 2.8 Zwartość 53
• 2.9 Ważne przestrzenie topologiczne 54
  • 2.9.1 Zbiór Cantora 54
  • 2.9.2 Kontinua 55
  • 2.9.3 Rozmaitości 59
• 2.10 Homotopia 62

3. Topologiczna filozofia 65

• 3.1 Topologia jako epistemologia: Kevin Kelly 65
  • 3.1.1 Poznanie ujęte w granicach 65
  • 3.1.2 Topologizacja przestrzeni empirycznych możliwości 66
  • 3.1.3 Topologiczne tło Kelly’ego: przestrzeń Baire’a 68
• 3.2 Topofilozofia Thomasa Mormanna 71
  • 3.2.1 Topologiczne tło rozważań metafizycznych 71
  • 3.2.2 Topologia jakości Thomasa Mormanna 73
• 3.3 Przymus topologizowania 75
  • 3.3.1 Marshall Stone: „One must always topologize” 75
  • 3.3.2 Ciągłość wcześniejsza od nieciągłości: Ren´e Thom 77
  • 3.3.3 Geometryczny model znaczenia Thoma 79
  • 3.3.4 Topologizowanie jest z istoty jakościowe 81
• 3.4 Topologiczna ontologia Janusza Kaczmarka 83
  • 3.4.1 Hermeneutyka topologiczna Kaczmarka 84
  • 3.4.2 Topologizacja monadologii 88
  • 3.4.3 Ile jest idei człowieka? Stopologizowane idee w ujęciu Kaczmarka 92
• 3.5 Topologia osoby Kurta Lewina 93
  • 3.5.1 Psychologiczna przestrzeń życia 94
  • 3.5.2 Pierwsze przybliżenie osoby 96
  • 3.5.3 Topologiczno-dynamiczna struktura osoby 100
  • 3.5.4 Wymiar przestrzeni życiowej? 104
  • 3.5.5 Metoda, krytyka i recepcja pomysłów Lewina 108
• 3.6 Topoontologia Benedykta Bornsteina 116
  • 3.6.1 Jakościowa geometria kategorialna Bornsteina 117
  • 3.6.2 Topologika Bornsteina 119
  • 3.6.3 Prawa topologiki nie okupują dziedzin bytowych, tyl¬ko je zamieszkują 120
  • 3.6.4 Dualność w geometrii rzutowej i w metafizyce 122
  • 3.6.5 Wyboiste ścieżki recepcji myśli Bornsteina 125
  • 3.6.6 Podsumowanie 128
• 3.7 Teoria katastrof Ren´e Thoma jako zmatematyzowana meta¬fizyka formy 130
  • 3.7.1 Katastrofy elementarne 134
  • 3.7.2 Teoria katastrof — zarys sformułowania matematycz¬nego 136
  • 3.7.3 Thom, topologia i Arystoteles 139
• 3.8 Topologia w nauce i technice 140
  • 3.8.1 Topologia w fizyce 141
  • 3.8.2 Topologia w robotyce 143
  • 3.8.3 Topologiczna analiza danych 144
  • 3.8.4 Topologiczny model umysłu Stanisława Janeczki 145
  • 3.8.5 Topologia sieci neuronalnej mózgu 146
  • 3.8.6 Topologiczne realizacje w ujęciu Daniela Kosticia oraz topologia sieci małego świata Wattsa-Strogatza 147
• 3.9 Czym jest topologiczna filozofia? 153
  • 3.9.1 Filozofia matematyczna 153
  • 3.9.2 Metafizyczne ugruntowanie filozofii topologicznej 153
  • 3.9.3 Jakości idealne i ideacja w ujęciu Romana Ingardena 156
  • 3.9.4 Żądło bąka dla gnuśnego konia: lekcja Sokratesa 168
  • 3.9.5 Topofilozofia w praktyce: spojrzenie kognitywistyczne 169
  • 3.9.6 Praktyka topofilozoficzna a transcendentalna fenome¬nologia pytająca 174
  • 3.9.7 Gigantomachia: spór o czyste jakości idealne? 176

4. Mereotopologia 180

• 4.1 Wprowadzenie 180
• 4.2 Mereologia a topologia 181
  • 4.2.1 Charakteryzacja topologiczna mereologii klasycznej 181
  • 4.2.2 Topologiczne ujęcie mereologii z sąsiedztwem 182
• 4.3 Mereotopologia jako teoria brzegów i części Barry’ego Smitha 185
  • 4.3.1 Składniki 186
  • 4.3.2 Części wewnętrzne 186
  • 4.3.3 Brzegi 187
  • 4.3.4 Topologia 188
  • 4.3.5 Ogólne uwagi do badań mereotopologicznych Smitha 189
• 4.4 Mereotopologia pierwszego rzędu Iana Pratt-Hartmanna 190
  • 4.4.1 Mereotopologia 191
  • 4.4.2 Geometryczna mereotopologia 191
  • 4.4.3 Przykłady mereotopologii 193
• 4.5 Uogólnienie mereotopologii: Breysse i De Glas 194
  • 4.5.1 Mereotopologiczne problemy z brzegami 194
  • 4.5.2 Lokologia jako próba rozwiązania problemów mereo¬topologii 196
  • 4.5.3 Lokologia jako nowa nauka o miejscu 201
• 4.6 Filozoficzna waga mereotopologii 202

5. Z historii zagadnienia część–całość 204

• 5.1 Platon 204
• 5.2 Arystoteles 211
• 5.3 Scholastycy 218
• 5.4 Jungius 221
• 5.5 Leibniz 223
• 5.6 Brentano 225
• 5.7 Twardowski 228
• 5.8 Ingarden 236

6. Teoria całości i części Husserla 244

• 6.1 Wprowadzenie 244
• 6.2 Podstawowe pojęcia 245
  • 6.2.1 Część 245
  • 6.2.2 Fenomeny samodzielności i niesamodzielności 246
  • 6.2.3 Ufundowanie, konkret, abstrakt 249
  • 6.2.4 Całość 251
  • 6.2.5 Jedność 253
• 6.3 Podstawowe twierdzenia 256
• 6.4 Formalizacja 259
  • 6.4.1 Potrzeba formalnego ujęcia teorii Husserla 259
  • 6.4.2 Symbolizacja Simonsa 261
  • 6.4.3 Formalizacja Rosiaka 262
  • 6.4.4 Formalizacja Fine’a 263
  • 6.4.5 Macierzowa reprezentacja: Blecksmith & Null 265
  • 6.4.6 Ku nowej formalizacji 270

7. W stronę ogólnej topoontologii przedmiotu i jego części 273

• 7.1 Rozważania wstępne 273
• 7.2 Preliminaria 274
• 7.3 Części 276
  • 7.3.1 Elementy 277
  • 7.3.2 Strony 277
  • 7.3.3 Kawałki 281
  • 7.3.4 Części formalne 282
• 7.4 Wymiar ontologiczny 284
• 7.5 Jedność 285
• 7.6 Spójność 287
• 7.7 Ufundowanie 288
• 7.8 Porównanie z innymi ujęciami 289
• 7.9 Pytania, problemy, perspektywy 297

8. Zakończenie 300

• 8.1 Wnioski 302
• 8.2 Dalsze drogi topoontologii 304
• 8.3 Problemy otwarte 305
• 8.4 Ostatni raz o wadze zagadnienia części i całości 306

Bibliografia 308

Indeks osobowy 331

[/tab]
[tab title=”Wprowadzenie”]

Wprowadzenie

0.1 Pierwsze intuicje

Wyobraźmy sobie taką sytuację: podczas spontanicznej rozmowy o naszych dzieciach jeden z kolegów prosi mnie, abym pokazał mu zdjęcie mojego syna. Odpowiadając, wyciągam smartfona i pokazuję mu wysokiej rozdzielczości zdjęcie, na którym widoczna jest sylwetka mojego syna, ale bez jego twarzy. Zakłopotaną minę rozmówcy można zauważyć natychmiast. W myśli mojego rozmówcy powstaje bowiem pytanie: przecież chciałem zobaczyć jego syna, a nie sylwetkę jego syna bez twarzy! Gdybym pokazał mu fotografię samej tylko twarzy syna, konsternacja ta nie miałaby miejsca. Niektóre części zatem są ważniejsze niż inne. A nawet niektóre części zastępują całość, na którą się składają — tak jak twarz (lub jej wygląd) zastępuje w określonych sytuacjach osobę (lub jej wygląd). Twarz jest zatem istotną częścią osoby, choćby w tym sensie, że jej utrata może doprowadzić do poważnej dezintegracji osoby. Tak jak usunięcie ucha filiżanki powoduje tylko tyle, że mamy do czynienia z uszczerbioną filiżanką, niemniej wciąż filiżanką, tak zupełne stłuczenie filiżanki i zmielenie części już ją w całości unicestwia. Niektóre części możemy usunąć z całości bez większego uszczerbku, niektóre zaś są istotne dla tej całości i przez to nieusuwalne. Ich usunięcie powoduje zniszczenie przedmiotu. Zainteresowany Czytelnik mógłby w tym miejscu podać przykłady takich przedmiotów, których wszystkie części są istotne. Tego typu przedmioty odegrały ważną rolę w naszej kulturze.

Rozważmy substancję chemiczną złożoną z dwóch atomów węgla, sześciu atomów wodoru oraz jednego atomu tlenu i naiwnie spytajmy, czym ona jest?^[1] Nie jest ona tylko prostym zestawieniem swoich części. W zależności od tego, jak te części zostaną strukturalnie rozmieszczone, jak ułożone są atomy, związek ten będzie alkoholem etylowym o wzorze CH₃CH₂OH bądź eterem dimetylowym o wzorze CH3OCH3. A to jest różnica. Struktura rozłożenia części i sposób składania się na całość ma istotne znaczenie nie tylko dla usypiających swe troski miłośników bezbarwnych cieczy o ostrym i palącym smaku. Aby wypracować podstawowe intuicje o tym, w jakim sensie mówię tutaj o strukturze, rozważmy jeszcze jedną sytuację, nieco zaskakującą, niemniej będzie to już ostatni eksperyment myślowy.

Przenieśmy się do krainy płaszczaków, czyli krainy stworzonej przez Edwina Abbotta, brytyjskiego pisarza, autora Flatlandii (zob. [1] oraz [75, s. 34-39]). Wyobraźmy sobie świat złożony z dużej kartki papieru. Jego mieszkańcy, odcinki, trójkąty, kwadraty, pięciokąty i inne figury mogą się swobodnie poruszać po tej kartce, ale nie mogą wyjść ani pod nią, ani ponad nią. Jak płaszczaki widzą siebie nawzajem?

Okrągła moneta na kartce widziana z góry wygląda jak koło, ale im bliżej jesteśmy kartki, im bardziej jesteśmy płaszczakami, tym bardziej figury wyglądają jak odcinki. Z krawędzi stołu każda figura wygląda jak odcinek. Kiedy płaszczak się zbliża do danej figury, to odcinek ten się po prostu wydłuża, kiedy płaszczak się oddala, to odcinek ten robi się krótszy. Dlatego płaszczaki się nie odróżniają, widzą tylko odcinki i nic więcej. Domy płaszczaków powinny zawierać co najmniej 5 boków, ponieważ domy kwadratowe, a tym bardziej trójkątne, posiadają zbyt ostre kąty, co mogłoby doprowadzić roztargnionego przechodnia do poważnego wypadku. W domach nie ma okien, światło oświetla zarówno wnętrza, jak i zewnętrza domów tak samo i bez względu na porę. Źródło światła pochodzi z przestrzeni, ale mieszkańcy Flatlandii nie znają przestrzeni. Uczeni z krainy płaszczaków, którzy próbowali wyjaśnić pochodzenie światła ze świata przestrzeni, trafili do domu dla obłąkanych.

Pewnego razu sfera wyławia kwadrat i zabiera go do przestrzeni. Sfera przechodząca przez Flatlandię widoczna jest początkowo jako punkt, następnie jako odcinek o coraz większych, a następnie coraz mniejszych rozmiarach, aż do zmniejszenia się znów do postaci punktu. Tylko tak sferę mogą widzieć mieszkańcy krainy płaszczaków. Kwadrat, który zobaczył trochę przestrzeni, zdając sobie sprawę z wcześniejszej bardzo ograniczonej, bo całkowicie płaskiej perspektywy, popada w zachwyt nad przestrzenią. Próbuje więc wyjaśnić płaszczakom, czym owa przestrzeń jest. Oczywiście zostaje okrzyknięty heretykiem, bo perspektywa przestrzenna istotnie wychodzi poza ramy perspektywy płaskiej. W świecie jednego wymiaru nikt nie chce słyszeć o świecie o dwóch wymiarach, w świecie dwóch wymiarów nikt nie chce słyszeć o świecie trzech wymiarów, i tak dalej. Niemniej z każdym wymiarem bogactwo możliwych sposobów bycia w przestrzeni wzrasta niepomiernie: w świecie jednowymiarowym mieszkańcy widzą tylko punkty, w świecie dwuwymiarowym widzą już odcinki, a w świecie trójwymiarowym figury posiadające — oprócz długości i szerokości — głębokość.

Doświadczenie niezrozumienia wyższego wymiaru, na przykład powszechne trudności w wyobrażeniu sobie czwartego wymiaru, potwierdzają intuicję Abbotta o wadze wymiaru danej przestrzeni. Wymiar przestrzeni jest własnością topologiczną, co oznacza, mówiąc jeszcze nieściśle, że nie zmienia się po odpowiednio zdefiniowanym przekształceniu danej przestrzeni. Przez to wymiar odróżnia przestrzenie od siebie, na przykład odróżnia prostą od powierzchni, a powierzchnię od przestrzeni trójwymiarowej. Wymiar stanowi różnicę. Jest istotną własnością struktury. Przez strukturę w tej książce rozumiem strukturę topologiczną. Innymi słowy zakładam, że struktura to w istocie topologia, przestrzeń to przestrzeń topologiczna, a immanentne i istotne charakterystyki przestrzeni to niezmienniki przekształceń topologicznych, o których więcej powiem za chwilę.

Książka ta jest przeglądem zagadnień, które z jednej strony dotyczą części i całości, a z drugiej dotykają strukturalnych charakterystyk, czyli własności topologicznych. Ontologia, w której decydujące są własności topologiczne, staje się ontologią topologiczną, w skrócie topoontologią. Filozofię, w której wykorzystuje się przestrzenno-topologiczne własności, nazywam topologiczną filozofią, w skrócie topofilozofią^[2].

Wyjściowym i głównym zagadnieniem jest problem części i całości. Zagadnienie to prowadzi wprost do teorii przedmiotu jako takiego. Idee części i całości należą do idei przedmiotu w ogóle, jak wykazał Husserl (zob. [134, s. 275]). Idea przedmiotu jest we współczesnej filozofii odpowiednikiem tego, co filozofowie w czasach wcześniejszych nazywali ens (zob. [454, s. 31-33]). Zmieniły się metody badania bytu, zamianie uległ również zakres tego pojęcia (zob. [293]), ontologom idzie jednak wciąż o jedno: czym właściwie jest to, co jest do pomyślenia i przedstawienia? Johannes Clauberg, niemiecki scholastyk i kartezjanista, którego dzieło Metaphysica de ente, quae rectius Ontosophia z roku 1664 uważane jest za bezpośrednią podstawę do powstania ontologii, nadawał w pierwszej kolejności terminowi ens właśnie takie znaczenie: cokolwiek da się pomyśleć, co jest czymś (aliquid), czemu przeciwstawia się nic (nihil) (zob. [293, s. 810-811]). Badanie zaś części przedmiotu oraz relacji wiążących bądź oddzielających te części, czyli relacji o charakterze ściśle topologicznym, jest formą badania samego przedmiotu. Powracam tym samym do źródeł samego filozofowania, do centralnego pytania ontologicznego: czym jest ens? Z rozważań zawartych w tej książce wyłania się pewna wizja ens — wizja topoontologiczna.

0.2 Metoda: filozofia topologiczna, w skrócie topofilozofia

Wiedza naukowa bywa porównywana do wnętrza koła: to, co jeszcze nie jest zbadane, jest na zewnątrz koła, to, co już jest poznane, jest wewnątrz koła, brzeg koła stanowi zaś granicę wiedzy i niewiedzy. Michał Heller rozwija tę metaforę:

Obwód tego koła tworzą więc pytania naukowe — problemy wyrastające z tego, co wiemy (z wnętrza koła), ale skierowane ku polu naszej niewiedzy (ku zewnętrzu koła). Wraz z postępem nauki, wraz ze wzrostem dokonań naukowych, koło symbolizujące wiedzę naukową poszerza się. Zauważmy jednak, że równocześnie powiększa się obwód tego koła — rośnie ilość znaków zapytania! [126, s. 7]

Jakub Jernajczyk wyraził tę intuicję odpowiednią ilustracją, którą przedstawiam na rysunku 0.1.

W stale rozpychającym się ku zewnętrzu kole, przeszukującym i eksplorującym przestrzeń niewiedzy, Kazimierz Twardowski odnalazł siłę ciągnącą do środka. W trakcie pierwszego zebrania Polskiego Towarzystwa Filozoficznego miał bowiem powiedzieć:

Jak wszystkie promienie koła, choć z różnych wychodzą punktów obwodu, łączą i spotykają się w środku koła, tak i my chcemy, aby wszystkie kierunki pracy i poglądów filozoficznych w naszym Towarzystwie ku jednemu zmierzały celowi, ku wyświetleniu prawdy. [453, s. 214]

Działanie dwóch sił: od wnętrza do zewnętrza oraz od zewnętrza do wnętrza przedstawia rysunek 0.2.

Krytyczny Czytelnik od razu pomyśli: o co chodzi? Przecież to są tylko metafory językowe i wizualne. W tej książce twierdzę, że nie są to tylko metafory — czy to językowe, czy wizualne. Za tymi podobieństwami stoją topologiczno-przestrzenne jakości idealne. Rozwinę tę myśl, wprowadzając już teraz nieco bardziej szczegółowo do jakościowego i topologicznego sposobu myślenia.

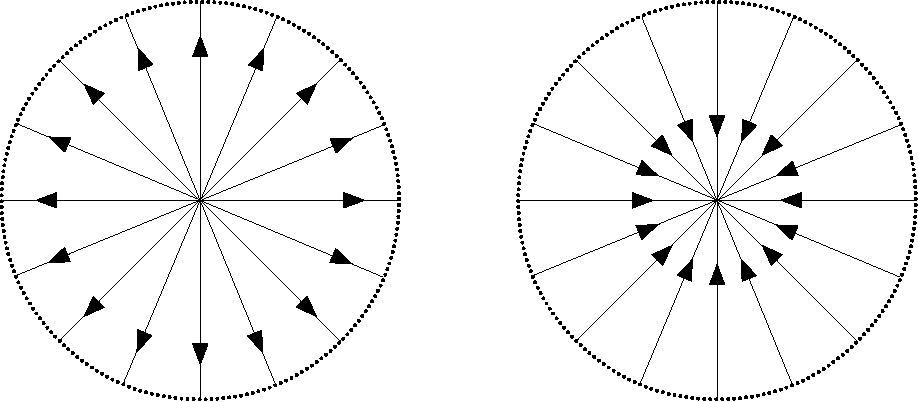
Krzywa zamknięta na płaszczyźnie bez samoprzecięć dzieli tę płaszczyznę na dwa obszary: wnętrze i zewnętrze, a sama jest brzegiem i jednego, i drugiego obszaru. To spostrzeżenie, które w matematyce jest nieoczywistym twierdzeniem Jordana (zob. [262, s. 27 i nast.}), wydaje się intuicyjne. Dzięki tej intuicyjnej własności każda krzywa topologicznie identyczna z okręgiem rozcina płaszczyznę na wnętrze i zewnętrze, będąc ich wspólnym brzegiem. Wnętrze, zewnętrze oraz brzeg są pewnymi splotami jakości idealnych, jak tutaj twierdzę, i to dzięki temu właśnie jakości te mogą się uobecniać, czy to w języku, czy to wizualnie, czy to idealnie w indywidualnych przedmiotach matematycznych. Topologiczna filozofia, do której usilnie wracam, ponieważ to ona jest właściwą metodą proponowaną w tej książce, to filozofia ufundowana właśnie na takim przekonaniu: przestrzenno-topologiczne sploty jakości uobecniają się w wielu różnych dziedzinach przedmiotowych, niezależnie od właściwego im sposobu istnienia. Prawa rządzące zaś jakościami przestrzennymi badane są przez topologów, stąd topologiczna filozofia czyni użytek z rozpoznań topologów, odnajdując konkretyzacje topologicznych własności w zagadnieniach filozoficznych. W tym sensie topofilozofia jest filozofią jakości, a nie ilości. Ilość zresztą w powszechnym mniemaniu jest błędnie kojarzona z matematyką i jej uprawianiem, podczas gdy wiele badań matematycznych w ogóle nie dotyczy ilości. Topofilozofia jest skupiona w pierwszym rzędzie na jakościach, które są dostępne między innymi w — rozumianej po Ingardenowsku — intuicji ejdetycznej. Intuicja ta, będąc wglądem w pierwotne związki między jakościami idealnymi (zob. [142, s. 324]), ma pierwszeństwo przed wszelkim formalizowaniem. W sedno trafił Zbigniew Król:

Chodzi jednak o prostą sprawę: jeśli weźmiemy np. podręcznik geometrii i zobaczymy tam definicję kuli i określone twierdzenia, to obok formalnych znaczków z topologii czy teorii miary niektórzy ludzie — co chcę wyraźnie podkreślić — wykażą również pozaformalne zrozumienie tego, czym jest kula. Umożliwia to sformułowanie szeregu prawdziwych twierdzeń dotyczących takiej kuli uzyskanych na pozaformalnej, intuicyjnej, drodze. [202, s. 11]

W praktyce często topofilozofia polega na wykorzystaniu narzędzi topologicznych do celów filozoficznych, nie to jest jednak jej istotą. Tak samo jak nie jest istotą filozofii matematycznej tylko stosowanie matematycznych narzędzi, jak czasem twierdzą w pośpiechu sami filozofowie matematyczni (zob. [227]). To może wyróżnia filozofię matematyczną i o niej wiele mówi, a w tym i to, że jest ona ścisła, niemniej nie jest ona matematyczna tylko z tego powodu. Ingarden był ścisły, a stosunkowo rzadko używał języka matematyki. Filozofia matematyczna jest matematyczna, ponieważ opiera się na odpowiednich zestawach jakości matematycznych, które dzięki podobieństwu z jakościami filozoficznymi uprawomocniają jej praktykę. Filozofia matematyczna to filozofia myślenia strukturami matematycznymi, których uposażenia jakościowe przypominają uposażenia jakościowe struktur filozoficznych. Jeśli rozważane struktury filozoficzne mają coś wspólnego z matematycznymi, wtedy siła intuicji ejdetycznej połączona z siłą matematycznego rozumienia i rozumowania napiera na granice filozoficznego koła. Koła pulsującego na obrzeżach filozoficznej wiedzy i ignorancji, a często też na styku filozoficznej mądrości i głupoty. Jeśli zaś struktury matematyczne rozmijają się z filozoficznymi, to powstała nieadekwatna konstrukcja formalna jest co najwyżej karykaturą. Słusznie wtedy mądrzy się z niej śmieją.

Wrócę jeszcze na chwilę do krzywej rozcinającej płaszczyznę. Gdy rozważymy takie krzywe na torusie, to okazuje się, że wtedy już nie wszystkie krzywe rozcinają torus na wnętrze i zewnętrze: niektóre krzywe zamknięte to robią, a niektóre nie. Niech przykładem torusa będzie dętka: narysowany na dętce okrąg (na przykład wokół małej dziury po przebiciu dętki) dzieli powierzchnię torusa na wnętrze i zewnętrze tego okręgu. Ale już kiedy wyobrazimy sobie krzywą idącą wzdłuż przecięcia dętki nożycami w poprzek czy wzdłuż, nie dzieli ona powierzchni na wnętrze i zewnętrze. Krzywą wokół dziury na torusie oraz przecięcie w poprzek torusa obrazuje rysunek 0.3. Raz jeszcze nie bez znaczenia jest fakt, w jakiej jesteśmy przestrzeni topologicznej: dętka i płaszczyzna nie są topologicznie identyczne.

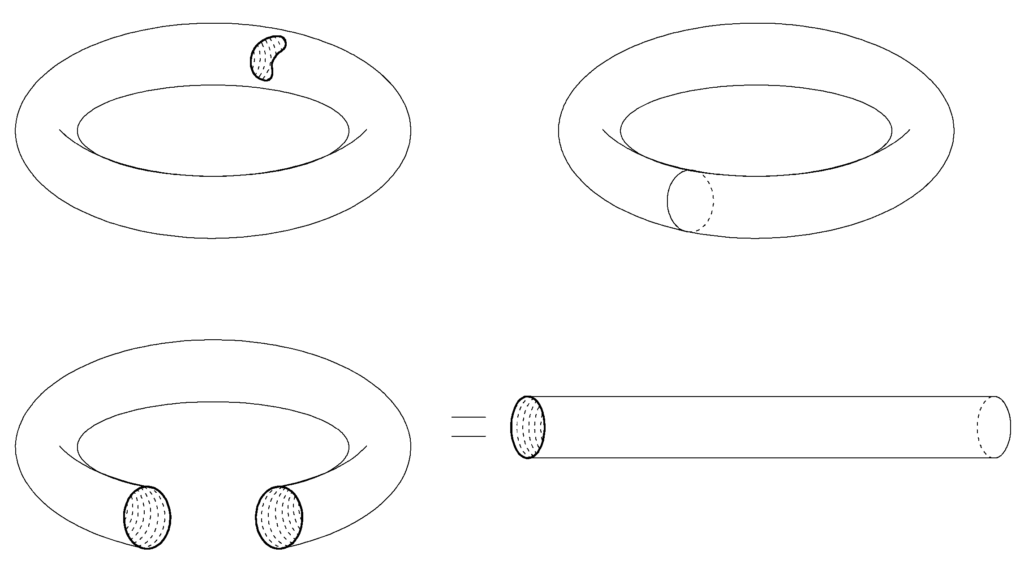
Topologia czyni ważną różnicę. A własności topologiczne, czyli własności przenoszone przez bijektywne obustronnie ciągłe przekształcenia, nazywane technicznie homeomorfizmami, pomiędzy przestrzeniami topologicznymi, stają się własnościami o wysokiej randze ontologicznej. Książka ta w zamyśle jest zachętą do topologizowania w filozofii, a w szczególności w ontologii. Innymi słowy zapraszam Czytelnika do myślenia w sposób jakościowy i przestrzenny, gdzie przestrzeń rozumiana jest szeroko, czyli jako przestrzeń topologiczna.

Wymiar przestrzeni, spójność przestrzeni, zwartość przestrzeni, liczba składowych spójności przestrzeni — wszystkie te własności nie ulegają zmianie po homeomorficznym przekształceniu, choć już kształt i własności metryczne mogą się zmieniać. Topologia jest geometrią gumy. Obrazowo mówiąc, wszystko, co można przekształcić bez rozrywania i sklejania, jest identyczne z punktu widzenia topologii. W ten sposób litery alfabetu, traktowane jako podzbiory płaszczyzny euklidesowej, można topologicznie sklasyfikować. Dla przykładu litery: C, I, J, L, M, N, S, U, W oraz Z są topologicznie tym samym: topolog nie widzi różnicy. Ważne jest to, aby litery te były przedstawione w kroju bez ozdobników, czyli w bezszeryfowej postaci o prostych końcówkach, w innym przypadku topolog tę różnicę może zobaczyć. Rozważmy realne modele liter zrobione z gumki. Wtedy w łatwy sposób bez klejenia i rozrywania z każdej z wymienionych można ułożyć każdą kolejną. Wystarczy odpowiednio ściągać i rozciągać gumkę. Są one homeomorficzne, jak powiedziałby topolog. Nie jest jednak możliwe takie przekształcenie w przypadku liter I oraz Y: stąd one nie są homeomorficzne. Litery I oraz Y różnią się między innymi tym, że gdy w literze Y usuniemy punkt połączenia wszystkich jej odnóg, to rozpadnie się ona na trzy Y części, czyli na trzy składowe spójności, a w literze I nie istnieje taki punkt, który rozspójniłby ją na trzy części. Punkty krańcowe nie dzielą w ogóle litery a dowolny punkt środkowy dzieli I tylko na dwie ! części. Stąd nie jest możliwy homeomorfizm pomiędzy tymi literami, ponieważ homeomorfizmy przenoszą liczbę składowych. Dla topologa zatem nie liczą się kształty, tylko wewnętrzne, jakościowe, topologiczne własności. Stąd też o topologach żartuje się często, że nie odróżniają kubka do kawy z jednym uchem od dętki, ponieważ jedno z drugim jest topologicznie identyczne. Poglądowo homeomorfizm ten oddaje rysunek 4. Uderzająco ujął topologiczność, zwracając uwagę na to, że to nie rozmiar w topologii jest ważny, Kurt Lewin [236, s. 88]: „nie ma topologicznej różnicy między kroplą wody a kulą wielkości Słońca”.

Filozofia, a w szczególności jej część teoretyczna, jest zbyt trudna, aby posługiwać się tylko zdrowym rozsądkiem i powszechnym rozumem. Filozofowanie wymaga bogatych i nieoczywistych struktur. Struktury te są tworzywem poznania filozoficznego, ważną jego częścią, nie zastąpią jednak samego poznania. W tym miejscu dochodzi do głosu druga z metod: ingardenizująca fenomenologia. Jako że intuicja ejdetyczna prowadzi nas w rozpoznaniu kolejnych zestawów skonkretyzowanych jakości idealnych, to uprawianie ontologii topologicznej jest w istocie analizowaniem zawartości odpowiednich idei, a w tym idei części, idei całości, idei przedmiotu, idei jedności, idei ufundowania, idei samodzielności, idei miejsca. Ontologia topologiczna rozważa i zestawia zawartości tych idei z zawartościami idei przestrzeni topologicznej, idei spójności, idei podprzestrzeni, idei brzegu, idei gęstości, idei wymiaru, idei domknięcia topologicznego itd. Oczywiście idee te rozważamy w oderwaniu od istnienia i nieistnienia ich przedmiotów, co najwyżej w nastawieniu ontologicznym badamy możliwość ich istnienia oraz samo istnienie, a nie istniejące przedmioty. W przedstawionej tutaj topoontologii (oraz szerzej topofilozofii) pobrzmiewać zatem będzie dwugłos ingardenizującej fenomenologii i metod topologicznych.

Artur Schopenhauer [359, s. 36-37] konfrontacyjnie zestawił poetę z filozofem. Poeta wprawia w ruch i ożywia bujną fantazją obrazy życia, ludzkie charaktery i przeróżne sytuacje. Przez to przynosi wiele radości i zadowolenia, rosną też w oczach kręgi jego przyjaciół. Filozof zaś przedstawia gotowe, wyabstrahowane myśli z owego życia czy owych sytuacji. Nie są one już tak żywo zabarwione. Filozof, wymagając od Czytelnika, aby ten myślał tak samo i doszedł równie daleko, zawęża też krąg możliwych odbiorców. Poeta bawi i podnosi na duchu, filozof zaś oczekuje od Czytelnika, aby bez skrupułów przeorał swoje dotychczasowe przekonania, porzucił je, uznając je za błędne, i rozpoczął na nowo poszukiwania. Krótko mówiąc, wedle Schopenhauera, poeta to ktoś, kto przynosi kwiaty, a filozof to ten, który przynosi ich ekstrakt. W tej książce sposobem na przyrządzenie owego ekstraktu, niezależnie od jego (nie)strawności i (nie)popularności, jest topologizowanie kierowane intuicją ejdetyczną. Zapewne także z nakreślonych tu powodów Janusz Kaczmarek w recenzji tej książki stwierdził o niej, że „jest książką trudną, nawet bardzo trudną”. Rozprawa recenzenta [163] nie różni się pod tym względem od mojej. Pozostaje nam tylko nadzieja, że — jak głosi porzekadło — choć są one trudne, to nie są nudne.

Współczesność odbiera rozumowi jego właściwe miejsce. Rozum jest dzisiaj zagrożony, jak mawiał Józef Maria Bocheński (zob. [36, s. 138], por. też uwagi Rene Thoma [448, s. 7-8] o filozofach jako strażnikach racjonalności oraz myśli Schopenhauera [359, s. 40-41] o wahadle pomiędzy obiektywnym i subiektywnym źródłem poznania). Książka ta wpisuje się w ten obszar działalności filozoficznej, gdzie broni się logosu — próbując z niego korzystać. Ponoć kogo on nie prowadzi, tego musi wlec. Ontologia i filozofia formalna, niezależnie od różnorodności jej wyników, jest miejscem współczesnych filozofów-racjonalistów.

0.3 Przegląd treści rozdziałów

Rozdział pierwszy poświęcony jest omówieniu mereologii, czyli formalnej teorii części; w tym mereologii klasycznej w duchu Stanisława Leśniewskiego oraz zauważonej przez Alfreda Tarskiego jej bliskiej relacji z algebrą Boole’a. Podobieństwo to sprawia, że z perspektywy ontologicznej mereologia klasyczna wymaga uzupełnień i dalszych rozwinięć. Przytaczam szereg faktów o mereologii rozszerzonej o relacje sąsiedztwa oraz omawiam krótko metodę rozciągłej abstrakcji Whiteheada, w której w nastawieniu bezpunktowym przyjmuje się za pierwotne rozciągłe obiekty, aby później przy pomocy odpowiednich konstrukcji niejako odzyskiwać punkty. Następnie prezentuję kategoryjne uogólnienie mereologii zaproponowane przez Thomasa Mormanna. Okazuje się, że jeśli jako model stosunku części do całości wykorzystamy kategoryjny stosunek podobiektu, każda kategoria posiadać będzie właściwą dla siebie mereologię. W ten sposób można z jednej strony badać mereologię ponad kategoriami, z drugiej badać jej strukturę w konkretnych kategoriach. W kategorii zbiorów mereologia ta jest algebrą Boole’a, niemniej już w innych kategoriach nie musi być algebrą Boole’a. Jako że ta kategoryjna aktualizacja mereologii przekracza kategorie, to wraca ona do starożytnych intuicji: część i całość, podobnie jak prawda, byt i jedność są transcendentaliami.

Rozdział drugi jest przeglądem podstawowych pojęć i metod używanych we współczesnej topologii. Obok pojęć i twierdzeń topologicznych, elementarnych z punktu widzenia pracującego matematyka, podaję wiele konkretnych przykładów przestrzeni topologicznych oraz odpowiednich własności topologicznych. Różnorodność, bogactwo, wręcz swoisty mnogościowy przepych struktur topologicznych sprawia, że każdy wybór struktur jest dowolny. Wybieram te struktury i przykłady, które uznaję za ciekawe i niosące potencjał ontologiczny. I tak przytaczam definicje przestrzeni topologicznej, bazy przestrzeni oraz przestrzeni metrycznej. Podaję wiele przykładów tych przestrzeni, mając nadzieję, że wyrobię u Czytelnika właściwe przekonanie o ontologicznym bogactwie struktur topologicznych. Omawiam też w elementarny sposób wnętrze, domknięcie, topologiczną gęstość i nigdziegęstość, pojęcie brzegu, zbiory regularnie otwarte, kilka rodzajów spójności i niespójności oraz zwartość.

Ważną własnością ontologiczną jest możliwość podziału danego przedmiotu, ona bowiem składa się na jego rozciągłość — nie muszę Czytelnika przekonywać o filozoficznej wadze zagadnienia przedmiotów rozciągłych i nierozciągłych. Już od najdawniejszych czasów filozofowie twierdzili, że continuum (zatem też ważne kategorie czasu i przestrzeni, które miały mieć strukturę continuum) wyróżnia się tym, że każda jego część jest też continuum oraz że continuum jest niewyczerpywalne w sensie podziału: można je dzielić w nieskończoność. Topologia zagadnienie podziału danego przedmiotu analizuje na wiele sposobów: mogą to być podprzestrzenie wyjściowej przestrzeni, może to być własność jednorodności przestrzeni, bycia jakby wszędzie taką samą, może to być rozkład na składowe spójności, jak w przypadku omawianych liter Y oraz I, może to być wreszcie zagadnienie możliwych topologicznych szwów oddzielalności części od siebie. Fenomen możliwych spoin przedmiotu szczegółowo ujmują kolejne aksjomaty oddzielania, które w istocie wychwytują ontologicznie doniosłe różnice. Na tych różnicach Kartezjusz opierał swoje przekonania o różnicy pomiędzy rzeczą a myślą. Stąd omawiam kolejne aksjomaty oddzielania, wskazując na przykłady odpowiednich przestrzeni spełniających te aksjomaty. Przytaczam definicję i przykłady przekształceń ciągłych oraz homeomorfizmów.

Często spotyka się opinie, że topologia jest nauką o ciągłości. Twierdził tak ontolog Jerzy Perzanowski [303]. Topolog Stefan Jackowski [149, §1] stwierdza:

Nadanie precyzyjnego sensu intuicyjnemu pojęciu ciągłości jest jednym z głównych tematów dziedziny matematyki, zwanej topologią.

Krótko wskazuję na kilka własności rozmaitości topologicznych, które uzupełniane różnymi strukturami, na przykład różniczkowymi, prowadzą do bogatych struktur matematycznych znów o wysokiej doniosłości ontologicznej (o czym świadczy choćby rola rozmaitości we współczesnej fizyce), oraz krótko omawiam wagę homotopii, czyli jednego z najbardziej elementarnych, a przez to też przystępnych narzędzi niezwykle już rozwiniętej topologii algebraicznej. Krótko omawiam także topologiczną teorię kontinuów, która rozwijana była przy dużym udziale polskich topologów i która może stanowić podstawę wielu przyszłych badań topoontologicznych.

Teoria kontinuów, która intensywnie rozwijana była podobnie jak logika matematyczna w pierwszej połowie XX wieku, nie została niemalże w ogóle zauważona w szerokich kołach filozoficznych. Topolodzy zajęli się metafizyką, a metafizycy tego nawet nie zauważyli. Wprawdzie nie będzie to żadnym pocieszeniem, niemniej być może choć trochę poprawi humor metafizykom, że podobne przeoczenie miało miejsce w biologii. Znajomość między innymi topologii bywa kluczem w zrozumieniu biologicznych procesów kształtotworzenia. Niemniej geometryczny sposób myślenia nie wniknął tak głęboko w środowisko biologów zajmujących się biologią rozwoju (informacje te podaję za Antonim Ogorzałkiem [282]), co doprowadziło do tego, że amerykański biolog F.T. Lewis (nie mylić z Davidem Lewisem), autor wielu prac o geometrii morfogenezy roślin publikowanych w latach 19231972, odkrył w istocie na nowo słynną charakterystykę Eulera powierzchni wielościanów (zob. słowa V.M. Maresina w [282, s. 316]). Co następnie V.M. Maresin skomentował następująco: „Wcześniejsza znajomość (…) zaoszczędziłaby mu wiele lat jego owocnych i pionierskich badań dotyczących przestrzennej organizacji tkanek biologicznych” (cyt. za [282, s. 316]).

Rozdział trzeci jest zasadniczy dla tej książki. Jest to przegląd zagadnień, w których jakości filozoficzne pokrywają się z jakościami topologicznymi. Rozpoczynam od oryginalnej i intrygującej topologizacji epistemologii Kevina Kelly’ego. Może to zaskoczyć, ale autor ten pokazał, że w ważnym sensie topologia może służyć za ogólną epistemologię. Falsyfikowalność idzie ręka w rękę z niebyciem gęstym, a obalalność z domkniętością. Wszystko to odbywa się w przestrzeni Baire’a. Następnie przechodzę do omówienia struktury topologicznej jakości w ujęciu Thomasa Mormanna. Przywołuję kluczową dla topoontologii maksymę topologiczną sformułowaną przez Mormanna oraz przywołuję motto Marshalla Stone’a: One must always topologize. Przedstawiam też szereg inspirujących, czasem kontrowersyjnych myśli metodologicznych (na przykład, aby myślenie ilościami zastąpić myśleniem jakościami, lub stwierdzenie, że rozumienie to geometryzowanie) i ontologicznych (na przykład myśl o pierwotności ontologicznej continuum) Rene Thoma, wielkiego topologa i zamaszystego i odważnego filozofa, na którego ważne pomysły zwrócił mi uwagę Zbigniew Semadeni. Rozmowy zaś ze Stanisławem Janeczko — wytrawnym znawcą zaawansowanych konstrukcji Thoma wzmocniły moje wyjściowe przekonanie, że myśl Thoma wciąż czeka na właściwą recepcję wśród ontologów i metafizyków.

Następnie prezentuję topologiczną hermeneutykę najprężniej działającego współcześnie topoontologa w Polsce: Janusza Kaczmarka. Hermeneutyka topologiczna inspirowana jest hermeneutyką logiczną Bogusława Wolniewicza. Omawiam część wyników Kaczmarka z zakresu topologizacji monadologii Leibniza. Dużą część rozdziału poświęcam topologii osoby autorstwa Kurta Lewina, który już w latach 30. XX wieku zauważył wagę różnic topologicznych. Wykorzystał podstawowe intuicje topologiczne i intuicje z zakresu fizycznej teorii pola, i na tej podstawie stworzył najciekawszą ze wszystkich mi znanych teorię osobowości. Prace Lewina stanowią dla mnie niewyczerpywalne źródło genialnych intuicji. Niemało miejsca poświęcam także na przedstawienie zapomnianych prac metafizycznych Benedykta Bornsteina, chyba najwybitniejszego polskiego topometafizyka. Bornstein antycypował filozoficzne założenia wielu osiągnięć intelektualnych wieku XX. Choć jego prace dopiero w ostatnich latach zaczynają być odkrywane, zestawienie jego topometafizyki z ontologią z Traktatu Wittgensteina wypada na niekorzyść tego drugiego, niezależnie od tego, co w szerokich kołach filozoficznych się mniema. Bornstein jako pierwszy spośród Polaków rozpoznał wagę metafizyczną rozmaitości i oparł swoją metafizykę na dwuwymiarowej i nieorientowalnej rozmaitości, jaką jest płaszczyzna rzutowa. Prace Bornsteina matematycznie nie wnoszą nic nowego, trzeba się zgodzić z jego krytykami w tym aspekcie, niemniej krytyka ze strony filozofów, z jaką się spotkał, stanowi groteskowy i nieco zabawny rozdział historii polskiej filozofii.

Kolejnym bohaterem rozdziału trzeciego jest wspominany już Rene Thom oraz jego teoria, a w zasadzie metafizyka formy matematycznej, która niefortunnie, choć dzięki temu zyskała na popularności, nazywana jest teorią katastrof. Bez wątpienia jest to najlepiej opracowana matematycznie topoontologia. Porywa jej bogactwo i uwypuklone różnice na styku ciągłości i skoku. Jej wartość została zauważona w naukach przyrodniczych i technicznych, niemniej znów oderwani metafizycy przespali powstanie i rozwój jednej z największych teorii formy — porównywalnej do osiągnięć Romana Ingardena z zakresu ontologii formalnej. Thom swoją głęboką i przejrzystą myślą ożywił i, jak sądzę, będzie dalej ożywiał metafizykę w duchu Arystotelesa.

Zjawiska topologiczne rozpoznawane są w wielu dziedzinach wiedzy: od matematyki, poprzez fizykę, chemię i biologię, aż do nauk technicznych, a także społecznych i humanistycznych. Stąd zdecydowałem się do rozdziału trzeciego dołączyć krótki i nieco hasłowy przegląd zastosowań topologii w nauce. Rozpoczynam od topologii w fizyce: aktualnie w zasadzie co kilka dni jest publikowana praca w jakimś porządnym czasopiśmie fizycznym^[3], wykorzystująca w sposób istotny zjawiska topologiczne. Wobec rozmaitości tych zastosowań i moich ograniczonych kompetencji hasłowo wspominam tylko kilka, po czym przechodzę do robotyki, a następnie omawiam topologiczną analizę danych: wyrażam nadzieję, że bądź to formalni, bądź tak zwani eksperymentalni filozofowie, jeżeli jeszcze w ogóle są filozofami, wykorzystają kiedyś te techniki. Cyfryzacja współczesnego świata doprowadziła do produkowania niespotykanej w tak dużej skali ilości danych. Okazuje się, że nowoczesne metody analizy danych wykorzystują też narzędzia topologiczno-algebraiczne, w tym badania nad trwałością homologii, które tam przywołuję i przystępnie, bez szczegółów technicznych, opisuję.

Następnie omawiam koncepcję umysłu autorstwa Stanisława Janeczki. W tej koncepcji topologiczne rozmaitości odgrywają kluczową rolę. Wierzę, że bogactwo matematyczne rozmaitości, które wykorzystał Janeczko, zdeterminuje przyszłe badania nad umysłem i mózgiem, wypierając aktualne trendy ujmujące mózg (a zatem też w domyśle umysł) jako sieć. Niezależnie od tego przekonania opisuję topologię sieci neuronalnej mózgu, która okazuje się być zbliżona do tak zwanych sieci małego świata, które wprowadzili Duncan Watts oraz Steven Strogatz, robiąc furorę w nauce. Topologia tych sieci jest wszechobecna we współczesnej praktyce naukowej, stąd dołączyłem jej opis do tego rozdziału. W ramach filozoficznej inżynierii wstecznej, jak to często bywa, część filozofów zastanawia się, na czym polega istota wykorzystania na przykład wyjaśnień topologicznych we współczesnej nauce. Nurt topologicznych wyjaśnień ożywił w ostatnich latach Daniel Kostić wraz z grupą współpracowników, wyciągając zresztą z urodzajnej metafizycznometodologicznej szafy Bornsteina dawne duchy, stąd poświęcam i jego pomysłom trochę miejsca.

Ostatnią już częścią rozdziału trzeciego jest próba odpowiedzi na pytanie, czym właściwie jest topologiczna filozofia. Wykorzystuję w tym miejscu pomysły, które opracowałem wspólnie z Krzysztofem Wójtowiczem w artykule o roboczym tytule The Metaphysical Foundations of Mathematical Philosophy. Twierdzę, o czym już wzmiankowałem, ale chcę to powtórzyć, że filozofia topologiczna zasadza się na pokrywaniu się zestawów jakości idealnych: matematycznych z filozoficznymi. Przekonanie, że matematyka jest tylko językiem nauki, jest przekonaniem z gruntu nieprawdziwym. Matematyka dostarcza systematycznych rozpoznań określonych zestawów jakości idealnych i jeśli się tak zdarzy, że podobne zestawy zostaną skonkretyzowane w dziedzinie bytu realnego, to wtedy poznanie jest poznaniem utrafionym.

Język, system aksjomatyczny itd. są wtórne w stosunku do jakości idealnych, a przez to, że są wszechobecne, sprawiają tylko wrażenie, że są najważniejsze. Niemniej pozajęzykowa i pozaaksjomatyczna rzeczywistość jest nieskończenie bogatsza i to ona wiedzie ontologiczny prym. W tym duchu, może zbyt wyraźnie tutaj zakreślonym, odpowiadam na pytanie, czym jest i czym powinna być topofilozofia.

Pod koniec rozdziału trzeciego przywołuję wielkiego mistrza: Sokratesa. W obronie rozumu powinniśmy pamiętać, aby sokratejskim młotem, choćby dla ćwiczenia, rozbić wytworzone siatki pojęciowe i wpuścić tam nieco nieporządku i powietrza. Wykorzystuję w tym celu rozważania kognitywistów. Pełny formalizm bowiem, pomimo swego uroku i pociągającej ścisłości, potrafi wodzić za nos filozofów — postępował też tak wielokrotnie ze mną — prowadząc tym samym do dusznych przestrzeni dogmatyzmu, gdzie jakże pożądana głębia okazuje się tylko poznawczą mgłą, jeśli nie błotem. Stanisław Lec nieuczesanie mawiał, że Bioto stwarza czasem pozory głębi, a I słowo może być kneblem [226, s. 6, 21]. Stąd filozofia topologiczna winna być nie na słowie oparta, tylko na intuicji, a najlepiej intuicji ejdetycznej.

W rozdziale czwartym wracam do form współgrania mereologii i topologii, omawiając część wyników badań nad mereotopologią. Nauka ta wciąż powstaje, nie ma zatem powszechnie przyjętych standardów prezentacji. Omawiam wpierw interpretacje topologiczne mereologii i mereologii z sąsiedztwem, aby później omówić badania mereotopologiczne Barry’ego Smitha, i w końcu dojść do pełnej teoretycznej konstytucji mereotopologii, to znaczy zdefiniowaniu mereotopologii za Ianem Pratt-Hartmannem z matematyczną ścisłością. Następnie, wskazując na kłopoty z topologicznym pojęciem brzegu, przedstawiam bardzo ciekawe uogólnienia mereotopologii zaproponowane przez Olivię Breysse i Michaela De Glasa. Uogólnienie to pozwoliło na wprowadzenie wielu różnic w warstwach brzegowych przedmiotu, w tym na przykład powłoki zewnętrznej i powłoki wewnętrznej. Doniosłość ontologiczną mają również fenomeny rdzenia i cienia, które autorzy także wyróżnili w przedmiocie. Swoje podejście nazwali podejściem lokologicznym — jest to kolejny już przykład, w którym wyjściowe zagadnienia mereologiczne kierują się w stronę technik teorii kategorii. Teoria kategorii z perspektywy galaktycznej przygląda się współczesnej matematyce, uwypuklając głębokie związki pomiędzy odległymi dziedzinami matematyki oraz wskazując na dynamiczny aspekt rzekomo nieruchomego świata matematyki. W naturalny zatem sposób pojawia się też w badaniach mereologicznych.

Rozdział piąty Z historii zagadnienia część-całość służy temu, by nie tracić kontaktu z filozoficznością zagadnienia części i całości. Brak kontaktu z zagadnieniami filozoficznymi często zarzuca się filozofom formalnym. Rozdział ten jest przeglądem tego, co istotne w próbach zrozumienia kwestii głównej. Przedstawiam w nim schematycznie wybrane myśli filozofów starożytnych, w tym dwóch największych: Platona i Arystotelesa, ale także wspominam o pracy — coraz częściej docenianych — scholastyków, a w tym: Gerlanda, Piotra Abelarda, Rajmunda Lullusa, Radulphusa Brito i Alberta z Saksonii. Następnie przedstawiam pewną wersję monadologii Leibniza, aby przejść do omówienia teorii całości i części dwóch polskich wielkich filozofów: Kazimierza Twardowskiego i Romana Ingardena. Rozdział ten jest wycinkiem ontologicznego bogactwa ukrytego w filozoficznym zagadnieniu części i całości.

Rozdział szósty poświęciłem filozoficznie chyba najbardziej dojrzałemu i wyrafinowanemu podejściu do zagadnienia całości i jej części, to znaczy teorii Edmunda Husserla wyłożonej w przełomowych Badaniach logicznych. Husserl potraktował zagadnienie części i całości na tyle obszernie, że zdecydowałem się jego wynikom poświęcić cały rozdział. Wprowadzam wszystkie ważne dla jego teorii pojęcia: części samodzielne, niesamodzielne, kawałki momenty, fenomeny ufundowania, jedność i jej rodzaje, bycie oddzielnym, rzecz, całość ekstensywną itd. Przywołuję także znane tezy Husserla o całościach i częściach. Omawiam w tym rozdziale również próby formalizacji teorii Husserla, twierdząc jednocześnie, że zagadnienie to wciąż pozostaje sprawą otwartą. W szczególności przywołuję próby formalizacji Simonsa, Rosiaka oraz Fine’a i Blecksmitha & Nulla. Propozycje Fine’a uznaję za najbliższą intuicjom Husserla. Fine bowiem odnalazł podobieństwo jakości topologicznej domkniętości z jakością ontologiczną ufundowania: a to właśnie tego typu podobieństwa wyróżniam i faworyzuję w tej książce. Być może pewne wskazówki do właściwego rozwiązania problemu formalizacji teorii Husserla znajdują się w rozdziale następnym, który jest próbą zbudowania ogólnej topoontologicznej teorii przedmiotu i jego części.

W rozdziale siódmym przedstawiam inne niż do tej pory uogólnienie i pełne stopologizowanie zagadnienia całości i jej części. Teoria ta jest wersją ontologii kombinacyjnej (ale nie kombinatorycznej!) w sensie Perzanowskiego [301]. Kombinacje elementów przybierają strukturę topologii. Przedmiot zaś w całości jest rozważany jako produkt wszystkich możliwych topologii, które nazywam stronami, związanych topologią Tichonowa. Przedstawiona teoria korzysta z wielu narzędzi topologii ogólnej. Jest z jednej strony tak ogólna, że prawdopodobnie skutecznie zniechęci wielu filozofów do podjęcia próby jej krytycznego rozważenia, z drugiej strony zaś dzięki jej ogólności możliwe są, jak sądzę, jej dalsze zastosowania w ontologii.

0.4 Potencjalny odbiorca książki

Wrocławski pisarz i miłośnik filozofii Marek Krajewski uświadomił mi, choć już niestety po tym, jak pierwsza wersja tej książki była gotowa, że autor książki powinien myśleć przede wszystkim o jej potencjalnym Czytelniku. Przyznaję, że nie było to dla mnie oczywiste. Wydaje się też, że nie jest to oczywiste dla wielu filozofów^[4]. Zacząłem się więc zastanawiać, kto mógłby być potencjalnym czytelnikiem.

Książka ta jest skierowana przede wszystkim do ontologów i metafizyków o formalno-racjonalistycznej orientacji. Jej przeglądowy charakter sprawia, że może ona służyć zarówno jako pierwszy kontakt z topoontologią (oby nie ostatni!), jak i jako ściąga dla wytrawnych badaczy, która w skrócie prezentuje rozmaitość pomysłów, obfitość formalnych ujęć i w każdym przypadku odsyła do bardziej zaawansowanych prac. Ontologów formalnych, którzy swoją pracę opierają na narzędziach współczesnej logiki, chciałbym przekonać, by myśleć strukturami, przede wszystkim topologiczno-przestrzennymi. Wreszcie liczę, że topoontologia znajdzie swoje właściwe miejsce wśród fenomenologów, w szczególności że sposób jej ujęcia, jaki proponuję tutaj, jest z ducha (choć nie z litery) ingardenizujący. Za metafizyczną podstawę topofilozofii przyjmuję jakości idealne, które są podstawowym materiałem Ingardenowskiej ontologii, a w tym też — skonkretyzowanym w zawartościach — tworzywem idei.

Matematyk raczej nie zainteresuje się sprawami tutaj poruszanymi, choćby dlatego, że nie podaję żadnych nowych twierdzeń matematycznych. W tej książce nie ma nowych wyników formalnych. Dowody zamieszczone we wcześniejszych wersjach książki w kolejnych wersjach usuwałem, ponieważ z każdym konferencyjnym wystąpieniem topoontologicznym, zdawałem sobie sprawę z tego, jak bardzo odległy jest żargon topologiczny od współczesnego języka ontologii. Topoontologia nie była zrozumiała (patrz historia recepcji myśli Bornsteina, którą omawiam w §3.6) i wciąż taka pozostaje. Matematyk nie ma czego szukać: wytrawni badacze jakości idealnych, bo tak widzę robotę matematyka, interesują się przede wszystkim niebanalnymi rozumowaniami (ponieważ intuicji ejdetycznej nie można przekazać, a narzędzia do przekazywania rozumowań we współczesnej matematyce są wyjątkowo ostre i skuteczne). Niemniej matematyk o metafizycznym usposobieniu może się bądź ucieszyć, bądź oburzyć w związku z tym, jak wiele wspólnego ma metafizyka i topologia. Reakcja zależeć będzie od tego, z której tradycji metafizycznej się wywodzi, jak i od tego, do którego kolektywu myślowego należy. Być może część matematyków zajmujących się matematyką stosowaną mogłaby zainteresować się zastosowaniem topologii w filozofii. Obawy jednak budzi panujący naturalizm w naukach szczegółowych, który często utrudnia zauważenie tak nieoczywistych zastosowań. Pochopnie i na skróty wielu sądzi bowiem, że humanistyka nie ma wiele wspólnego z matematyką. Niemniej tylko odrobina życzliwości wystarczy, by przyjąć perspektywę topoontologiczną i uznać ją za być może dziwaczną i matematycznie nieciekawą, ale jednak poznawczo doniosłą. W końcu matematycy być może mogliby po przestudiowaniu tej książki pomiarkować, dlaczego Platon wymagał znajomości geometrii od adeptów filozofii. Może zatem współczesna geometria powinna wrócić do programu studiów filozoficznych?

Zdawszy sobie sprawę z wagi sugestii Krajewskiego, nie próbując pisać książki zupełnie od nowa, dokonywałem wielu zmian w trakcie kolejnych redakcji. Zmiany te w zamierzeniu miały uczynić tekst przystępniejszym w odbiorze. Nowe media oraz nowe technologie sprawiły, że zsieciowana w wirtualności uwaga Czytelnika, a w szczególności tego wychowanego od młodości na YouTubie, nie znosi zbyt długich wywodów, a tekst chciałaby mieć podany w interaktywnej formie wizualnej, jeśli nie multimedialnej. Głębokich zmian w architekturze poznawczej, których jesteśmy świadkami, nie oceniam w tym miejscu (zob. [394]), niemniej zupełnie poważnie je traktuję. Dlatego też książkę ozdobiłem wieloma ilustracjami. Na szczęście topologia, jak i geometria, dobrze reagują na ilustracje. Z pewnością jednak mogłoby być ich więcej.

0.5 Topoontologia w Polsce w XXI wieku

Książka ta powstawała ponad 10 lat. Poszukiwania podobieństw między ontologią i topologią rozpocząłem z dwóch powodów: pierwszym było doświadczenie równoległego studiowania topologii i ontologii/metafizyki. Bez właściwego rozpoznania, nieco na ślepo, już jako student miałem wrażenie, że zarówno topolog, jak i metafizyk często mówią o tym samym. Podkreślają wagę tych samych różnic. Nierzadko używają różnych siatek pojęciowych oraz często robią to w zupełnym oderwaniu od siebie. Następnie Marek Magdziak, wprowadzając mnie w meandry współczesnej ontologii formalnej, jak i filozofii w ogóle, nierzadko w duchu wielkiego Platona, przekazał mi teczkę wydrukowanych artykułów, w których między innymi Barry Smith oraz Peter Simons wskazywali na wzajemne relacje topologii i ontologii. Zachwyciłem się tymi relacjami i głębokimi podobieństwami: już wtedy kiełkował we mnie pomysł, aby wykorzystać rozpoznania topologów w filozofii. Wydawało mi się bowiem, że wiele fenomenów ontologicznych dogłębnie i systematycznie oni zbadali. Dużo pracy zostało wykonane i wyniki czekają gotowe do wykorzystania. Przygotowałem doktorat, na którym oparta jest ta książka, dotyczący mereotopologicznych aspektów filozoficznej teorii całości i części pod opieką Jacka Hawranka i Marka Magdziaka. Doktorat obroniłem w roku 2012 na Uniwersytecie Wrocławskim. W roku 2011, dzięki wsparciu Katedry Logiki i Metodologii UWr., kierowanej wtedy przez Jana Zygmunta, odbyłem kwerendę w The British Library w Londynie, gdzie zapoznałem się z najnowszą literaturą i gdzie rodziły się pierwsze pomysły topoontologiczne. Tymczasem nawiązałem wieloletnią współpracę z Thomasem Mormannem. Wciąż jego prace uważam za bardzo ważny wkład do topoontologii w wieku XXI.

W roku 2016 współorganizowałem konferencję Topological Philosophy oraz szkołę dla studentów i doktorantów wprowadzającą do topologicznej filozofii. W konferencji tej wzięli udział m.in.: Tomasz Bigaj, Samuel Fletcher, Rafał Gruszczyński, Janusz Kaczmarek, Marek Kuś, Thomas Mor- mann, Tomasz Placek, Ian Pratt-Hartmann, Peter Simons, Achille C. Varzi oraz Roland Zarzycki. Od roku 2018 zacieśniłem współpracę z aktualnie najaktywniejszym i pełnym inicjatyw topoontologiem w Polsce, Januszem Kaczmarkiem. Współpracowaliśmy w ramach kierowanego przez niego projektu finansowanego ze środków Narodowego Centrum Nauki: Atom. Substancja. System. Badania z zakresu ontologii topologicznej o numerze 2017/27/B/HS1/02830. W związku z badaniami finansowanymi w tym projekcie powstały §3.3, §3.4 oraz §3.8 tej książki. Kolejne warsztaty z topologicznej filozofii zorganizowaliśmy wspólnie z Januszem Kaczmarkiem, Thomasem Mormannem oraz Frankiem Zenkerem w Donostia San Sebastian na Uniwersytecie Kraju Basków w roku 2020, zaraz przed wybuchem pandemii koronawirusa. W roku 2019 powstała grupa badawcza z topologicznej filozofii przy Międzynarodowym Centrum Ontologii Formalnej na Wydziale Administracji i Nauk Społecznych Politechniki Warszawskiej. W skład grupy weszli w kolejności alfabetycznej: Javier Belastegui, Rafał Gruszczyński, Janusz Kaczmarek, Marek Kuś, Wiesław Kubiś, Nasim Mahoozi, Thomas Mormann, Imanol Mozo, Grzegorz Sitek, Krzysztof Wójtowicz oraz Frank Zenker. Wielu z nich wywarło zarówno wpływ na moje badania, jak i na treść tej książki, co Czytelnik łatwo dostrzeże, ponieważ starałem się skrupulatnie to odnotowywać, przywołując stosowne ich prace.

W trakcie tych dziesięciu lat i w zakreślonym wyżej kolektywie myślowym powstawała ta książka. Pierwsza jej wersja, jak już wspomniałem, była doktoratem. Kolejne wersje różniły się od pierwszej zarówno redakcją tekstu, drobnymi uzupełnieniami, jak i gdzieniegdzie merytorycznie — w szczególności tam, gdzie uszczegóławiałem swoje stanowisko metafilozoficzne. Koncepcję ufundowania metafizycznego topologicznej filozofii w jakościach idealnych opracowałem wspólnie z Krzysztofem Wójtowiczem w roku 2020. Obszerny, liczący ponad sto stron rozdział trzeci, powstał na przełomie lat 2020 i 2021. Z każdym kolejnym rokiem dodawałem kolejne wątki i przykłady topologicznych rozumowań w ontologii i filozofii. Dlatego książka ta ma przede wszystkim charakter przeglądowy: zbiera dużą część wyników z zakresu topofilozofii, a w szczególności topoontologii i stanowi stosunkowo szeroką bazę odniesień do tekstów specjalistycznych.

0.7 Nota redakcyjna

Przyjmuję dwa sposoby wyróżniania definicji. Pierwszy sposób to wyróżnienie definicji z tekstu głównego (odstęp z góry i z dołu plus pochylenie tekstu definicji) wraz z podaniem jej numeru i często nazwy definiowanego pojęcia. Drugi sposób to podanie definicji w tekście głównym w ciągu. Wyraz definiowany (lub tylko objaśniany) wtedy pochylam. Pismem pochyłym wyróżniam tytuły prac i ich części, wyrazy obcojęzyczne oraz wyrażenia, które są przedmiotem opisu w tekście bądź stanowią egzemplifikację opisywanego zjawiska. Pochylenia też używam, gdy chcę podkreślić rolę danego wyrazu w zdaniu lub szczególną wagę jego znaczenia. Na czym ta waga polega, powinno być jasne z kontekstu. Pochylone są też symbole matematyczne, zgodnie ze standardem systemu LTEK. Odnośniki bibliograficzne podawane przy definicjach i twierdzeniach często odnoszą się nie do autorów tych definicji i twierdzeń, tylko do tekstów z których zaczerpnąłem dane twierdzenie. Gdzieniegdzie w tekście podaję, kto oryginalnie był autorem danego pojęcia lub twierdzenia — niemniej książka ta nie ma ambicji historycznych. Tam, gdzie było to możliwe, podawałem więcej niż jeden odnośnik, aby ułatwić Czytelnikowi dotarcie do danej treści i wskazać na wielość jej ujęć. Pogrubienia są stosowane do oznaczenia nazw rozdziałów i ich części, numerów rysunków oraz nazw definicji i twierdzeń i ich numerów porządkowych.

Bibliografia, niezależnie od często przyjmowanej praktyki, zawiera też te pozycje, które (w całości lub w części) na pewnym etapie przygotowywania tej książki wpłynęły na moje spostrzeganie danego zagadnienia, bez względu na to, czy wprost się do nich odwołuję w tekście. Dzieje się tak, gdy na przykład nie zgadzam się z danym autorem co do jakiejś treści. Nie zawsze przywołuję w tekście tę niezgodę, niemniej zakładam, że treść ta miała wpływ na mój sposób myślenia. Na przykład po zapoznaniu się z tekstem, którego tezy są dla mnie jawnie nieprawdziwe, utwierdzałem się często w swoim własnym przekonaniu. Stąd w bibliografii zostawiam ślad tego wpływu, przywołując tę pracę. Oczywiście nie każda praca, z której treścią się nie zgadzam, jest częścią bibliografii, jak i nie każda, która jest częścią bibliografii i nie jest przywoływana w tekście zasadniczym, jest przedmiotem niezgody. Bibliografia jest zatem — niezgodnie ze sztuką — szerokim sprawozdaniem z moich lektur, a czasem tylko sprawozdaniem z prób zrozumienia tylko ich fragmentów. Zdecydowałem się na taką formę sporządzania bibliografii, licząc na to, że tak szerokie zestawienie pozycji ułatwi w przyszłości pracę topofilozofów. Zebrałem bowiem w jednym miejscu wiele prac, które tworzą swoisty topofilozoficzny nastrój.

Gdy odnoszę się w pewnej części tej książki do innej jej części, wtedy piszę na przykład zob. §3.1.2, co oznacza, że odnoszę się do rozdziału 3, podrozdziału 1 oraz podpodrozdziału 2. Spis treści pozwala na szybką lokalizację zakresu stron rozdziałów i pod(pod)rozdziałów. Identyfikacja pozycji bibliograficznej, dla ułatwienia sprawnego poruszania się po stosunkowo obszernej bibliografii, następuje po numerze porządkowym. Gdy odnoszę się do pozycji bibliograficznej, na przykład [142, s. 299], to oznacza, że odnoszę się do strony 299 w pozycji bibliograficznej o numerze [142]. Czasem odnoszę się do rozdziałów danych pozycji, [12, §3] oznacza odniesienie do rozdziału 3 w pozycji bibliograficznej [12].

Czytelnik korzystający z wersji elektronicznej tej książki zapewne już zauważył, że podświetlony na magentowo link odsyła do odpowiedniego miejsca tej książki, na przykład xxviii odsyła do strony xxviii. Gdy odsyłacz jest podświetlony na niebiesko, to odsyła do treści zewnętrznych względem tej książki. Najczęściej niebieskie hiperłącze odsyła poprzez identyfikator cyfrowy DOI do miejsca opublikowania publikacji (w tym strony internetowej czasopisma) lub też do miejsca w przestrzeni wirtualnej, gdzie dana treść była zlokalizowania w trakcie przygotowywania książki (na przykład strony autora). Starałem się używać stabilnych adresów stron docelowych, niemniej bez wątpienia część z nich się przedawni i przestanie działać, zmuszając tym samym Czytelnika do samodzielnego przeszukiwania Internetu.

Stosuję dwa wyodrębnienia cytatów. Krótkie cytaty znajdują się w tekście zasadniczym w ciągu i są ujęte w cudzysłowy. Nie jest zmieniany rozmiar czcionki. Dłuższe cytaty wydzielam z tekstu głównego, zmniejszając rozmiar czcionki, zwiększając światło przed i po oraz dodając wcięcie po obu stronach. Tak wydzielonych bloków nie ujmuję w cudzysłowy.

Zwracam uwagę — często zajętego administracyjną codziennością współczesnej Akademii — Czytelnika, że wielopoziomowy spis treści zamieszczony w tej książce mógłby służyć do szybkiego przeskanowania treści tej książki. Podobnie jak wirtualna ściana na Facebooku służy zeskanowaniu najważniejszych aktualności. W zamieszczonym na końcu książki indeksie osobowym umieściłem ważniejsze nazwiska i imiona występujące zarówno w tekście głównym, jak i bibliografii. Indeks obejmuje także nazwiska występujące w nazwach twierdzeń i pojęć matematycznych, jak i w tytułach. Wielopoziomowy i szczegółowy spis treści wraz z obszernym indeksem osobowym, a także możliwość przeszukiwania opublikowanego w otwartym dostępie PDFa powinny zastąpić indeks rzeczowy.

Większa część części tej książki żyje osobnym życiem i nie potrzebuje do swojego istnienia innych części, co oznacza, że oprócz rozdziału czwartego i siódmego rozdziały mogą być czytane niezależnie od siebie. Pierwsi Czytelnicy książki wskazywali, że rozdział piąty zakreśla odpowiednie tło dla rozważań tej książki, stąd Czytelnik mógłby rozpocząć czytanie właśnie od tego rozdziału. Aby zapoznać się z głównym filozoficznym przesłaniem tej książki, przy minimalnym zaangażowaniu uwagi, wystarczy przeczytać kolejno rozdziały piąty, drugi, trzeci oraz siódmy. Wreszcie Czytelnik, który wyjściowo mniema, że topofilozofia jest niewiele warta, stąd też nie chce jej poświęcać swojej cennej energii mentalnej, wystarczy, że w swojej życzliwości przeczyta ze zrozumieniem tylko rozdział trzeci. Owo zrozumienie w mojej opinii powinno być dobrą podstawą do rewizji wyjściowego mniemania.

^[1]Przykłady pochodzą odpowiednio z [222, s. 88] oraz [198, s. 478] — zostały one nieznacznie dostosowane do celów wprowadzenia.

^[2] Topologiczne zastosowania w biologii nazywane są biologiczną topologią lub biotopologią (por. [341, s. 118]). Preferuję nazwę topoontologią, a nie ontotopologia, ponieważ idzie przede wszystkim o rozpoznania z zakresu ontologii — rozwój topologii zostawiam topologom.

^[3] Zobacz na przykład prace przywoływane w [131] — artykuł ten ukazał się kilka dni przed złożeniem tej książki do druku, zob. też [424].

^[4]Fakt ten stał się nawet przedmiotem żartów: matematyk do pracy potrzebuje kartki, ołówka i kosza, filozof zaś tym się od matematyka różni, że nie potrzebuje kosza.

[/tab]

[tab title=”Część i całość. W stronę topoontologii (eBook OPEN ACCES)”]

E-book jest opublikowany w OPEN ACCES, a egzemplarz drukowany można zamówić tutaj: http://www.wydawnictwopw.pl/index.php?s=karta&id=3711.

kliknij w okładkę i pobierz plik pdf

[/tab]

[/tabs]